Abstract

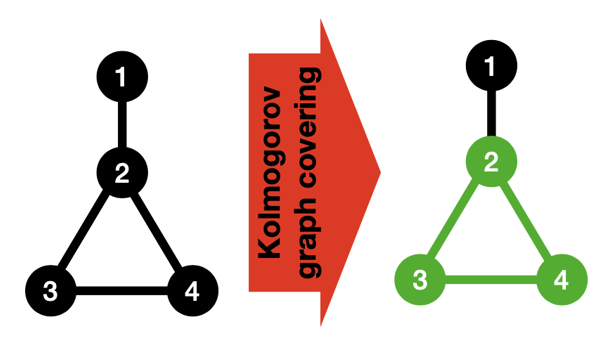
Throughout the years, measuring the complexity of networks and graphs has been of great interest to scientists. The Kolmogorov complexity is known as one of the most important tools to measure the complexity of an object. We formalized a method to calculate an upper bound for the Kolmogorov complexity of graphs and networks. Firstly, the most simple graphs possible, those with O(1) Kolmogorov complexity, were identified. These graphs were then used to develop a method to estimate the complexity of a given graph. The proposed method utilizes the simple structures within a graph to capture its non-randomness. This method is able to capture features that make a network closer to the more non-random end of the spectrum. The resulting algorithm takes a graph as an input and outputs an upper bound to its Kolmogorov complexity. This could be applicable in, for example evaluating the performances of graph compression methods.