Research Areas

Research Areas
Developing tools and algorithms for the analysis and design of feedback control in biological and technological systems
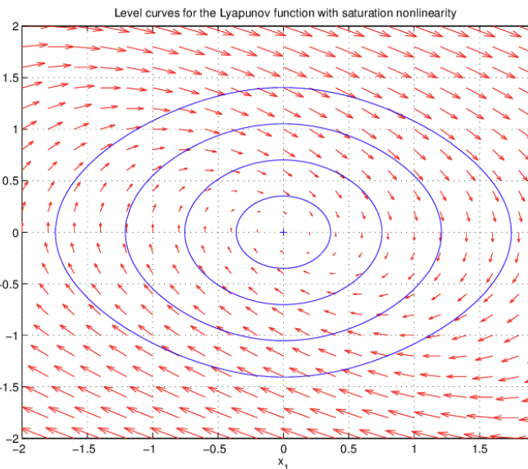
Non-linear systems, sum of squares optimisation & Lyapunov techniques
We have developed methods for stability analysis of systems described by ordinary, delay and partial differential equations, as well as switched/hybrid systems.
We are working to scale these tools to handle much more complicated and richer system descriptions of higher dimension.
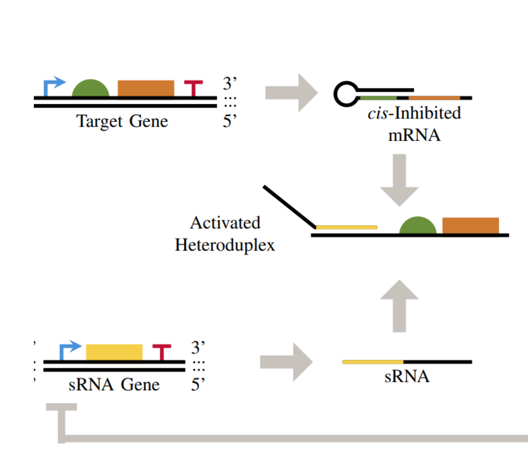
Systems & synthetic biology
We collaborate closely with other University research groups within engineering science (under Prof Wei Huang and Prof Harrison Steel) and biology (Prof Philip Poole), as well as with groups based at other institutions.
To understand biological pathways, we leverage mathematical modelling using experimental data and design new experiments for model invalidation ("systems biology").
We also propose and implement redesigns to existing biological systems to improve their performance ("synthetic biology").

Software development (SOSTOOLS)
SOSTOOLS is a free MATLAB toolbox for formulating and solving sums of squares (SOS) optimisation programmes.
SOSTOOLS can be used to specify and solve sum of squares polynomial problems using a very simple, flexible and intuitive high-level notation.

Large-scale networked systems
Our research investigates large-scale networked systems such as synchronisation phenomena in oscillator networks, network congestion control for the Internet, and power systems/smart grid analysis.
We also work on multi-agent systems consensus under communication and structural constraints, such as the effect of time delays or switching topologies.
Fluid mechanics & heat transfer
We use control engineering principles and approaches to interrogate hydrodynamic stability and mechanisms for background noise energy amplification and subsequent reduction.
We also apply a sum of squares approach to perform stability analysis and control the design of systems described by partial differential equations.

Complexity reduction of networked systems
We investigate methods based on model decomposition and reduction to facilitate computational analysis and identification of large-scale and non-linear systems.
Systems of particular interest include biochemical reaction networks, power systems, and consensus networks.
Scaling sum of squares and semidefinite programming
We employ sparsity- and symmetry-exploiting algorithms to improve the scalability of semidefinite programming, including developing software such as CDCS to implement relevant operator-splitting algorithms.
Robust analysis and design of (deep) neural network controllers
We use tools from traditional and modern control theory for the analysis and design of (deep) neural network controllers used in (deep) reinforcement learning.
