14 Mar 2023
Clarabel: An Interior Point Solver for Quadratic Conic Optimization
Spotlight on ongoing work by Yuwen Chen

Convex optimization is a powerful tool in many industries and lots of applications in control are optimization problems inherently, like linear quadratic controller (LQR) and model predictive control (MPC). It transforms a real-world problem into a mathematical model, which has a cost function with a bunch of constraints, which can be solved by a computational software, usually called a solver. However, the computational time grows fast when the dimension of a problem becomes larger and a speedy solver is usually needed, especially for those scenarios require a solution with time limit.
Recently, we developed a new solver called Clarabel, which is based on our new interior point method. It is originally written in Julia and Rust, but we also provide a Python wrapper for it based on the Rust version.
Our solver can solve conic problems including linear programming (LP), quadratic programming (QP), second-order, semidefinite, exponential, and power cones, which shares a general form as follows:
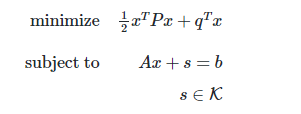
It works faster and more stable than the state-of-art open-source counterparts and the performance is comparable with commercial solvers like Gurobi and Mosek.
Wanna try it yourself? We have a supporting website https://oxfordcontrol.github.io/ClarabelDocs/stable/, which details how to build up your own optimization problem from the scratch in either Julia, Rust or Python.