Connecting Neural ODEs and Control

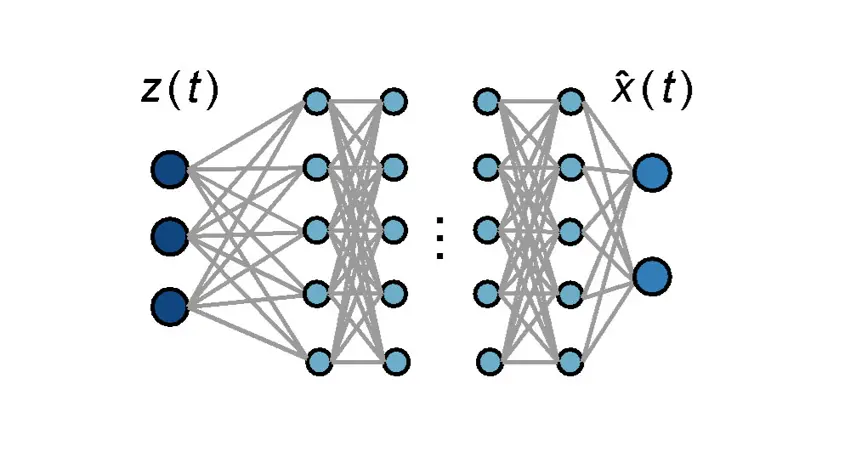
The combination of dynamic systems and deep learning has become a topic of great interest, and Neural ODEs is one work that can be considered a milestone which has built a bridge among neural networks, differential equations, and optimal control. This line of work can be seen as inspired by the control domain, providing a new perspective on the construction and training of neural networks, and demonstrating their superiority in many machine learning problems.

Recently, we established a connection between control theory and Neural ODEs, presenting a new approach for learning robust state observers of nonlinear systems based on traditional design methods such as KKL observers, which is a challenging problem in dynamic systems. Neural ODEs offer a powerful framework for modelling dynamic systems by embedding neural networks into ordinary differential equations. This approach enables end-to-end learning of observers, enhancing their performance and adaptability.

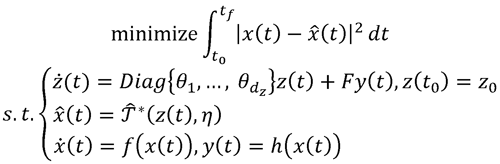
where Θ and η represent parameters of neural networks.

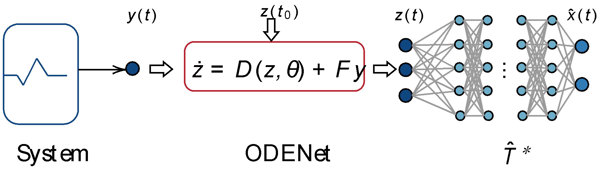
By analysing the robustness of the KKL observer, techniques such as regularisation are applied to develop robust state observers that exhibit resilience to uncertainty and noise, thereby enabling precise estimation of the system's internal states. More information can be found at https://proceedings.mlr.press/v211/miao23a/miao23a.pdf.

This work demonstrates a case where we aim to apply Neural ODEs back to the control domain and use it to solve many problems in dynamic systems. Meanwhile, we also have some ongoing work aiming to continue to improve on Neural ODEs from a control theory perspective and allow control theory to continue contributing to the field.