Prism: An Ultra-Precise FFT calculation

The Fast Fourier Transform (FFT) has been described as “the most important numerical algorithm of our lifetime”, used billions of times a day [1]. The FFT can be applied to 1-D data (sound recording or measurement signal) or 2-D data (photograph or medical image). It calculates the strength (or amplitude) of each frequency (e.g. sound pitch or image colour) contained in the data set. The method is applied in practically all branches of science and engineering.

 A new technique developed by Manus Henry of the Engineering Science Department addresses some of the well-known limitations of the FFT. The figure below shows various FFT analyses of a one second record of a simulated signal, sampled at 48 kHz. The signal contains three true tones (marked as ‘+’), at frequencies of approximately 8.95 kHz, 9.0 kHz, and 9.05kHz. The amplitude of the middle tone is only 1 microVolt, while the other tones are both around 1 Volt. The two dashed lines show conventional FFT results, and demonstrate the effect known as frequency leakage. The two strong tones create peaks in the spectra, but they also ‘leak’ into the surrounding frequencies, raising the noise floor so that the weak true tone cannot be observed. The higher dashed line is generated using the original FFT algorithm, and results in a noise floor of around 1 milliVolt. The lower dashed line uses the FFT after applying a windowing function (the “Hann” or “Hanning” window) to reduce spectral leakage, producing a noise floor of around 1 microVolt. The green and blue lines show results from the new Prism FFT technique. The noise floor is around 1 picoVolt and the middle tone is successfully detected.

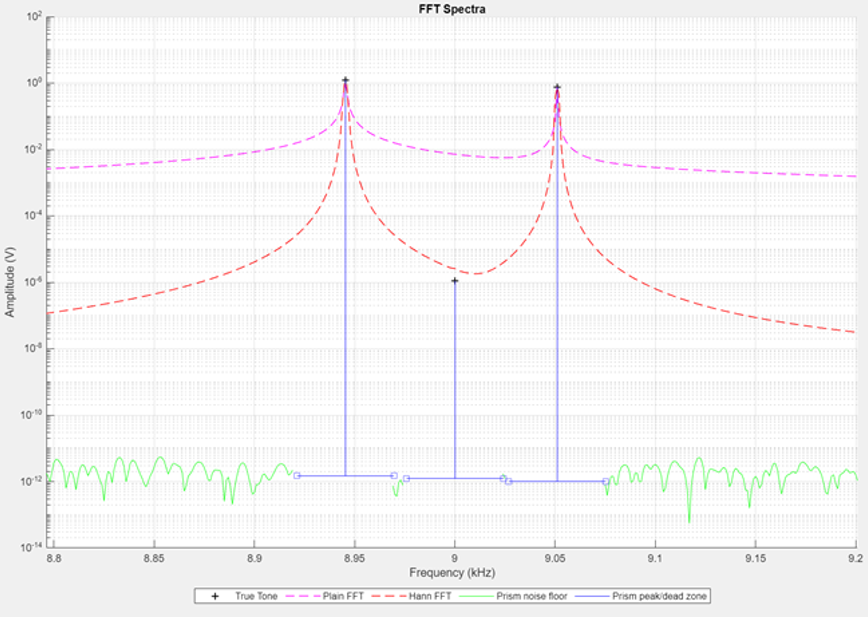
A further limitation of conventional FFT is the accuracy with which tone frequency and amplitude can be calculated. In this example, amplitude values are calculated in steps of 1 Hz, so that an estimate of tone frequency may have an error of up to 0.5 Hz, while the error in tone amplitude may be up to 30%.  By contrast, the Prism FFT technique uses two windowing functions to calculate the exact tone frequency and amplitude. In this example, the two outer tones are correctly calculated to 12 decimal places, while the middle tone is computed to 6 decimal places. These high precision results are achieved using only twice the computational cost of conventional FFT methods.

A patent for the new Prism FFT technique has been filed by Oxford University Innovation.

[1] Schneider, D. “A Faster Fast Fourier Transform”, IEEE Spectrum, March 2012.